圖片出處

我們都要有矢量（向量）操作能力

只是差別是，我們不需要像一方通行那樣，吸入必要的氧氣防止能力消失，我們學會了就可以操作！

向量一般來說，是指一個同時具有大小和方向，且滿足平行四邊形法則的幾何對象，在three.js裡面，向量變成一個物件的概念，也就是Vector2, Vector3, Vector4 等。在前面幾篇的介紹理，一定對向量的操作有所體悟，但今天我要打破你對向量在three.js與WebGL效能上的認知。

學一方通行在短時間內分析底層特性來反擊immutable

底層特性：向量構成了這個世界

在three.js，三維的向量稱作Vecor3存在於非常多地方，你的鏡頭位置、鏡頭方向、鏡頭縮放、鏡頭目標都是向量組成，再加上你場景上的所有物件。

底層特性：three.js的向量是不喜歡immutable的

three.js的世界裡有一個區塊是animate()，也就是JS裡面渲染的迴圈。在那個區域裡面，理想上一秒執行60次。如果你在JS渲染的迴圈裡面不斷實例化Vector3，那麼它將一直重新分配Vector3的記憶體位置。再加上場景本身已經有那麼多向量，很容易就會消耗非常多的CPU資源。

舉一個例子好了，今天你修改Vector3的X位置，修改後回傳了新的Vector3物件，導致記憶體重新分配了不只X的位置，還有Y、Z、整個Vector3的位置。雖然說看起來還好，但當你整個場景都是用向量構成，而且每一秒要重新分配60次的時候，這個問題就變得很大了。

於是，這造就了three.js為了最佳化效能，所應用的mutable模式。

底層特性：假設今天你要開發新的three.js

假設你今天是發明three.js的天才工程師，為了避免資源的浪費，你會怎麼設計你的程式呢？

//假設今天要相加兩個向量：
vectorA.add(vectorB) // 方法一、把相加結果加在A上
vectorA.add(vectorB) // 方法二、把相加結果加在B上
vectorA.add(vectorB) // 方法三、把相加結果加在新回傳的向量

雖然方法三才是最immutable的方法，這避免了潛在的javascript開發疏忽，可是如果它放在render()裡面，每次執行都要實例化新向量然後更換整個Vector3的記憶體位置，那就太浪費資源了，不行不行。

而方法A跟方法B相比，放在render裡面的話，好像都沒什麼差別。可是如果選A的話，可以讓函式像chain一樣一直加上去，好像不錯！那就選A好了！

於是乎大家都這樣設計向量的應用方式，你看隔壁棚跟three.js打對台的babylon.js也一樣這麼做。

不止向量，這概念遍佈three.js

跟Immutable概念相反，three.js的很多物件偏向mutable。亦即：物件內部的資訊會一直更動，而物件本身指向的記憶體位址不變。

而這都是效能的考量。

事實上，不止Vecotr3，這樣的概念到處可見。你一旦理解了，就更能快速的認知three.js的世界，成為three.js的一方通行。例如：

• Quaternion.multiply()
• Matrix4.copyPosition()
• Object3D.copy() （Object3D是Mesh, Group, Camera等物件的父類別）
• 還有很多

事實上你只要在three.js看到有關運算的函式，其運算結果基本上不會實例化新的物件！

不會實例化物件…那要把運算結果放哪裡？但它一定得找地方放計算結果，基本上就是將物件自己的數值換成計算結果。

必備的向量函式

這邊以vector3做介紹：

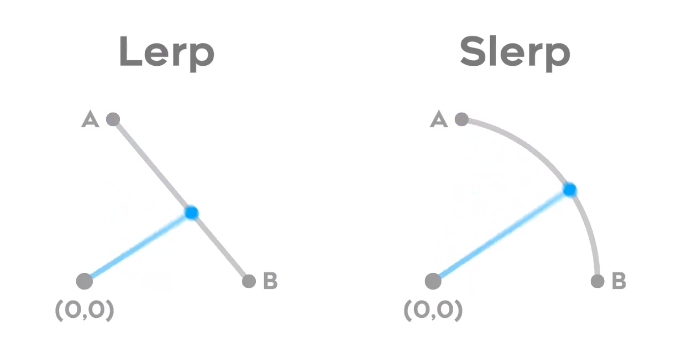
• .lerp()

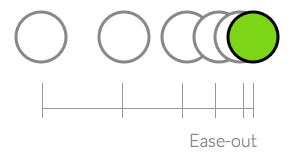
  執行一次就會往v2移動「一段距離」，第二個參數是百分比，定義移動多遠的距離。

  執行第二次時，會移動「剩下距離」的再一段距離。以此類推。

  以下面這個為例子，第一次執行時v1已經往v3移動了25%，第二次則是剩下距離(75

  5)的再25%。然後就會創造出類似ease-out的效果。

  

  圖片來源

  const v1 = new THREE.Vector3(0,0,0)
  const v2 = new THREE.Vector3(10,10,10)
  const a = v1.lerp(v2,0.25)
  console.log(a);
  // Vector3 {x: 2.5, y: 2.5, z: 2.5}
  

  • 順帶一提，四元數有slerp的函式，概念類似。

    

    圖片來源

• .addScalar()

  幫x,y,z各加上一個數。適合用在拉長一個長度的時候。

  const v = new THREE.Vector3(10,5,0)
  const a = v.addScalar(5)
  console.log(a);
  // Vector3 {x: 15, y: 10, z: 5}
  

• .addVectors()

  兩向量相加。

  const v1 = new THREE.Vector3(10,5,0)
  const v2 = new THREE.Vector3(2,6,4)
  const a = new THREE.Vector3(0,0,0).addVectors(v1, v2)
  console.log(a);
  // Vector3 {x: 12, y: 11, z: 4}
  

• .angleTo()

  取得兩向量角度

  const v1 = new THREE.Vector3(0,5,0)
  const v2 = new THREE.Vector3(5,0,0)
  const a = v1.angleTo(v2)
  console.log(a);
  // 1.5707963267948966
  // = 0.5 π
  

• .clampLength()

  提供上下界，如果達不到上下界，那向量就會被拉長到下界；反之，如果超過上界，那向量就會被壓縮到上界。

  const v = new THREE.Vector3(3,4,0)
  v.clampLength(10,12)
  console.log(v);
  // Vector3 {x: 6.000000000000001, y: 8, z: 0}
  

• .distanceTo()

  取得兩向量的距離

  const v1 = new THREE.Vector3(7,24,0)
  const v2 = new THREE.Vector3(14,48,0)
  const a = v1.distanceTo(v2)
  console.log(a);
  // 5
  

• .length()

  計算出向量的長度

  const v1 = new THREE.Vector3(5,12,0)
  const a = v1.length()
  console.log(a);
  // 13
  

• .multiplyScalar()

  向量被拉長N倍。

  const v = new THREE.Vector3(9,40,0)
  const a = v.multiplyScalar(2)
  console.log(a);
  // Vector3 {x: 18, y: 80, z: 0}
  

最推的向量函式

掌握了乘法就是控制了向量。

積（Product）就是「乘出來的結果」。Vector3提供兩個非常有用的工具，在應用網頁時解決我們數學上面的難題。

「積」如果是兩數字相乘的話，結果會是一個數字沒錯。但如果是兩個向量相乘，結果應該要是一個數值呢？還是另一個向量？都幾？

這個「乘」就有不同的作法。在三維向量的乘法中，有兩種最有名，最可以代表向量中的「積」。

那兩種中，有一種乘出來會是一個數字，有一種乘起來會是另外一個向量。

＊以下我們以單位向量（即長度為一單位的向量）來討論。

最推的向量函式：乘出來會是一個數字的那種

Vector3.dot()

可以代表兩個向量的關係。到底在一個空間中，兩條現有「多麼」相近呢？可以給我一個數字代表他們多相近嗎？如果有的話，就是用它了！

舉一個例子說明：假設你在開發開飛機遊戲好了，遊戲要求玩家往目標方向飛，但玩家飛偏了。那到底有多偏呢？玩家飛行方向跟目標方向有多麼相近？這時就可以用Vector3.dot()來表達。

Vector3.dot() 回傳的結果，兩向量越是相近，越是趨近於1。最終如果是同方向，那就是1。相反的，如果兩個向量越是相反，則越趨近-1，如果完全相反，那就是-1。概念很簡單吧？

有這麼一個數字可以代表兩個向量的關係，就可以在開發上解決很多問題了，並且更快做出很多效果了！

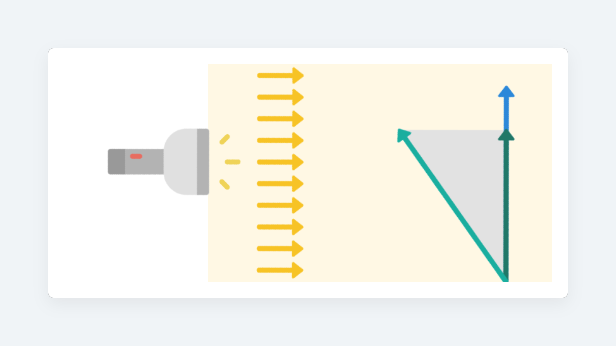
就很像在向量A垂直的方向開一盞燈，看向量B有多長一段長度可以投影在A身上。如果是垂直則沒有長度可投影（所以值呈0），如果平行則全部長度都可以投影，同方向是1，反方向是-1

const v1 = new THREE.Vector3(1,0,0)
const v2 = new THREE.Vector3(0.8,0.6,0)
const a = v1.dot(v2)
console.log(a);
// 0.8

最推的向量函式：乘起來會是另外一個向量的那種

Vector3.cross()

前一個方法能很快速的找到兩個向量的關係，但它終究是一個數字，沒辦法代表方向。可不可以給一個「積」是能告訴我兩個向量都面向哪裡，而且多麼相近啊？有的，就是用這種。

這個方法，可以得出一個公垂（亦即都垂直）於兩個向量的向量，於是我們就可以依據這個得出來的向量，觀察原本的兩者有多相近，而那兩者的公垂方向在哪裡。

Vector3.cross() 可呈現藍色部分的向量。A.corss(B)是製造一個公垂向量，同時垂直於A也垂直B。由此，我們不僅可以知道兩個向量多近，還可以透過這個公垂向量，去回推他們發生在哪一個面上。

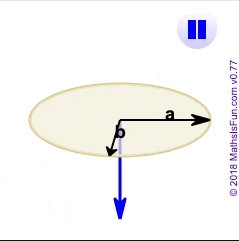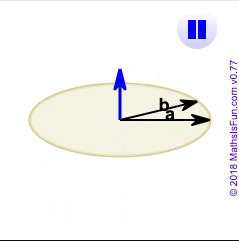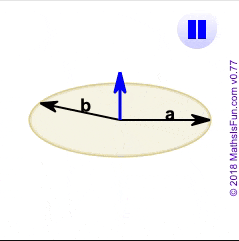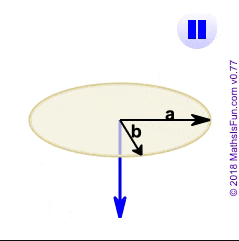
影片來自https://www.mathsisfun.com/algebra/vectors-cross-product.html

const v1 = new THREE.Vector3(1,0,0)
const v2 = new THREE.Vector3(0.8,0.6,0)
const a = v1.cross(v2)
console.log(a);
// Vector3 {x: 0, y: 0, z: 0.6}

最推的向量函式：這兩個積到底是何方神聖？

乘出來會是一個數字的那種 ，使用函式Vector3.dot() 。其中的「dot」一詞其實就是dot product的意思，dot product就是點積啦，也就是內積。

乘起來會是另外一個向量的那種，使用函式Vector3.cross() 。其中的「cross」一詞，其實就是cross product，也就是叉積。在三維空間中也可以稱它為外積。

• 由於它「公垂」兩個向量，所以他至少得存在於三維空間中，在二維空間中是不存在的。
• 而且，在四維空間中，有點積（dot）、外積（outer）、偶積（even）、叉積（cross）。所以在四維空間中不應稱之為外積，而是叉積。

參考資料

向量，乘就乘，為什麼要叫「內積」？

Dot Product

Cross Product

向量的定義

Section 5-3 : Dot Product

向量外積與四元數

Understanding the Dot Product and the Cross Product

為什麼three.js的vector是mutable的討論